The ternary quantization methods proposed in this paper based on threshold and quantized weights to 0 and {-1, +1} with two different scaling factor. The authors also suggested the rule of scaled gradient to update weight in different group. Quantized ternary weight $w_l^i$ of the network can be calculated by:
$$
w_l^t =
\begin{cases}
W_l^p&:& \tilde{w_l} \gt \triangle_l \\
0&:& |\tilde{w_l}| \le \triangle_l \\
-W_l^n&:& \tilde{w_l} \lt -\triangle_l
\end{cases} \tag{1}
$$
Different from previous work where weights are calculated from 32-bit weights, the scaling coefficients $W_l^p, W_l^n$ are two independent parameters and are trained with gradient descent:
$$
\frac{\partial L}{\partial W_l^p} = \sum_{i\in I_l^p}\frac{\partial L}{\partial w_l^t(i)}, \\
\frac{\partial L}{\partial W_l^n} = \sum_{i\in I_l^n}\frac{\partial L}{\partial w_l^t(i)}, \tag{2}
$$
Here $I_l^p={i|\tilde{w_l}(i) \gt \triangle_l}$ and $I_l^n={i|\tilde{w_l}(i) \lt -\triangle_l}$. The proposed scaled gradients for 32-bit are weights computed by:
$$
\frac{\partial L}{\partial\tilde{w_l}} =
\begin{cases}
W_l^p\times\frac{\partial L}{\partial w_l^t}&:&\tilde{w} \gt \triangle_l \\
1\times\frac{\partial L}{\partial w_l^t}&:&|\tilde{w}| \le \triangle_l \\
W_l^n\times\frac{\partial L}{\partial w_l^t}&:&\tilde{w} \lt -\triangle_l
\end{cases} \tag{3}
$$
Different from TWN, the authors explored two strategies to decide the values of thresholds: (1) $\triangle_l=t\times\max(|\tilde{w}|)$, $t$ is set to 0.05 on CIFAR-10 and ImageNet; (2) $\triangle_l=r$, where $r$ is a hyper-parameter and adjusted with various sparsities. For exploring the trade-off between sparsity and accuracy, the sparsity of weights are growing from 0 to 0.5 and the best result occurs with sparsity between 0.3 and 0.5.
Training Methods
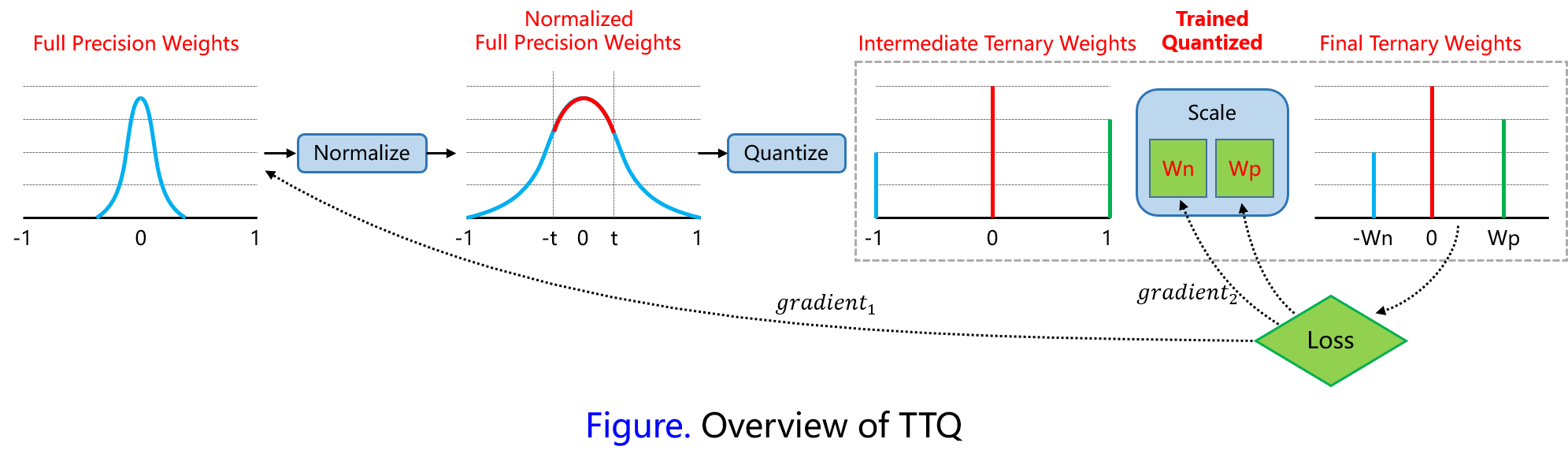
First: normalize full-precision weights to range $[-1, +1]$ by dividing each weight by the maximum weight
Second: quantize weights to ${-W_l^n, 0, W_l^p}$ with threshold factor $t$
Third: compute the scaled gradients and update the scaling coefficients with back propagation
Source code is available on GitHub.
Experimental results
Testing error on CIFAR-10 with ResNet is shown as follows:
| Model | Full precision | Trained Ternary Quantization | Improvement |
|---|---|---|---|
| ResNet-20 | 8.23 | 8.87 | -0.64 |
| ResNet-32 | 7.67 | 7.63 | 0.04 |
| ResNet-44 | 7.18 | 7.02 | 0.16 |
| ResNet-56 | 6.80 | 6.44 | 0.36 |
The authors further evaluate their method on ImageNet with AlexNet and ResNet-18B. To AlexNet, the authors preserves full precision weights in first convolutional layer and the last fully-connected layer, and other layer parameters are quantized to ternary values. Experimental results are shown as follows:
| Model | Bit-width | ImageNet Top-1/Top-5 Error | Accuracy Loss |
|---|---|---|---|
| AlexNet reference | 32 | 42.8 / 19.7 | - |
| AlexNet DoReFa | 1 | 46.1 / 23.7 | -3.3 / -4.0 |
| AlexNet TWN | 2 | 45.5 / 23.2 | -2.7 / -3.5 |
| AlexNet TTQ | 2 | 42.5 / 20.3 | -0.3 / -0.6 |
| ResNet-18B reference | 32 | 30.4 / 10.8 | - |
| ResNet-18B DoReFa | 1 | 39.2 / 17.0 | -8.8 / -6.2 |
| ResNet-18B TWN | 2 | 34.7 / 13.8 | -4.3 / -3.0 |
| ResNet-18B TTQ | 2 | 33.4 / 12.8 | -3.0 / -2.0 |