Paper: https://arxiv.org/abs/1712.05877
Code: refer to TensorFlowLite.quantize
Training with simulated quantization
Point-wise quantization:
$$
clamp(r;a,b) := min(max(r, a), b)
$$
$$
s(a,b,n) := \frac{b-a}{n-1}
$$
$$
q(r;a,b,n):=\lfloor \frac{clamp(r;a,b)-a}{s(a,b,n)} \rceil s(a,b,n)+a
$$
Here, $r$ represents the real value, $q$ represents the quantized value. $\lfloor \cdot \rceil$ denotes rounding to the nearest integer.
for weights: $a:=min(w), b:=max(w)$
for activation: collect [a;b] during training and aggregate them via exponential moving average (EMA)
1 | exponential moving average (EMA) in tensorflow: |
Note: activation quantization is disabled at the start of training
compute gradient
$$
\frac{\partial{L}}{\partial{r}} = \frac{\partial{L}}{\partial{q}}\frac{\partial{q}}{\partial{r}}
$$
Here, we have $\frac{\partial{q}}{\partial{r}}=0$ if $r\notin[a,b]$, otherwise $\frac{\partial{q}}{\partial{r}}=1$.
Inference with integer-arithmetic only
Data type
input: uint8
weights: uint8
bias: int32
activation: int32
output: uint8
Affine mapping from q to r
Formulation:
$$
r = S(q-Z) \to q=\frac{r}{S}+Z
$$
where $S$ means “Scale” and $Z$ means “Zero point”. And $S=s(a,b,n), Z=z(a,b,n)$.
Therefore, considering $r_3=r_1*r_2$:
$$
r_3 = S_3(q_3-Z_3), r_1*r_2=S_1S_2(q_1-Z_1)(q_2-Z_2)
$$
$$
q_3 = \frac{S_1S_2}{S_3}(q_1-Z_1)(q_2-Z_2)+Z_3
$$
Let $M:=\frac{S_1S_2}{S_3}$ and $M=2^{-n}M_0$, $M_0\in(0.5,1]$.
For matrix multiplication of two matrices with size of $N\times N$.
$$
q_3^{(i,k)} = Z_3 +M\sum_{j=1}^{N}(q_1^{(i,j)}-Z_1)(q_2^{(j,k)}-Z_2)
$$
It needs $O(N^3)$ subtraction to compute the result.
More efficient implementation:
$$
q_3^{(i,k)} = Z_3 + M(\sum_{j=1}^N q_1^{(i,j)}q_2^{(j,k)}-\sum_{j=1}^N q_1^{(i,j)}Z_2-\sum_{j=1}^N q_2^{(j,k)}Z_1 + \sum_{j=1}^N Z_1Z_2)
$$
$$
q_3^{(i,k)} = Z_3 + M(\sum_{j=1}^N q_1^{(i,j)}q_2^{(j,k)}-Z_2 \bar a_1^{(i)}- Z_1a_2^{(k)} + N Z_1Z_2),
$$
where $\bar a_1^{(i)}:=\sum_{j=1}^N q_1^{(i,j)}$ and $a_2^{(k)}:=\sum_{j=1}^N q_2^{(j,k)}$. Therefore, the computational costs is mainly from the computation of $\sum_{j=1}^N q_1^{(i,j)}q_2^{(j,k)}$
The Following operations
scale down: int32 activation –> int8 output activation
cast down: int8 activation –> uint8 output
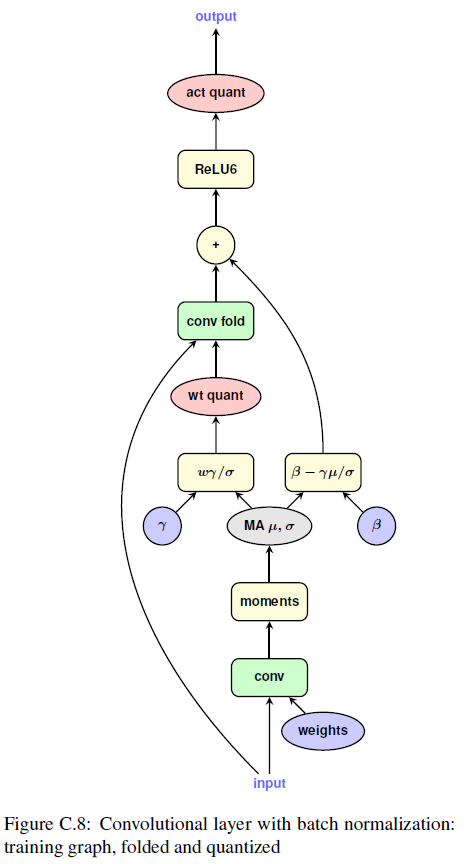
Batch normalization folding
$$
w_{fold}:=\frac{\gamma w}{\sqrt{EMA(\sigma_B^2)+\epsilon}}
$$
Graph illustration
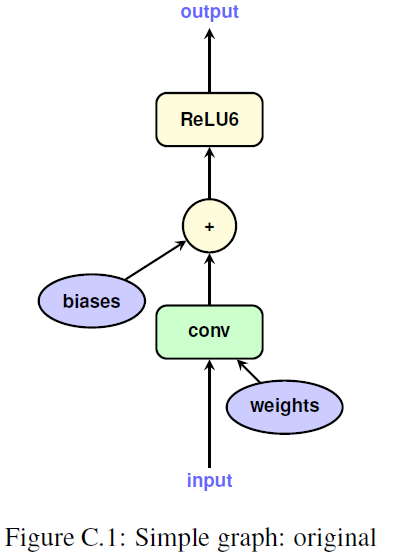
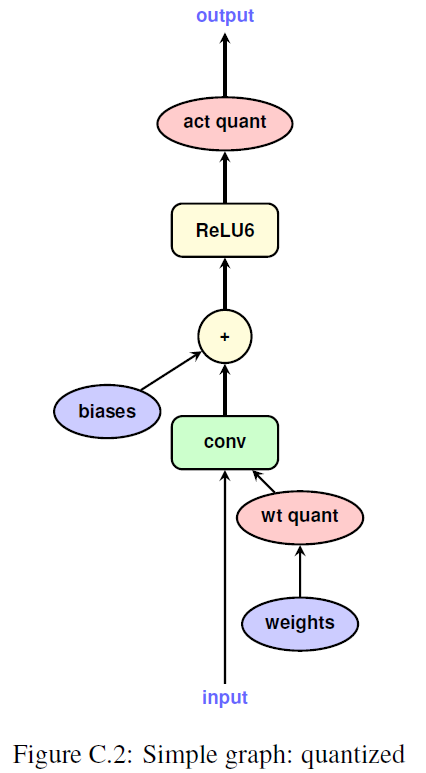
simple graph for single layer
- origin
- quantized
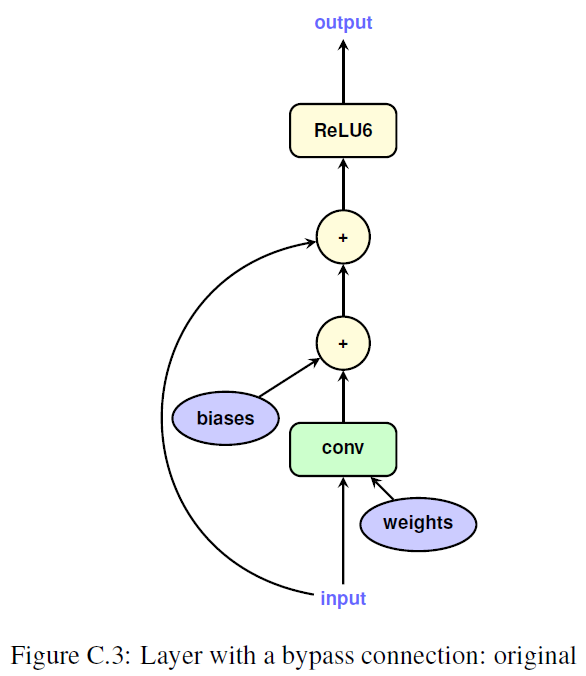
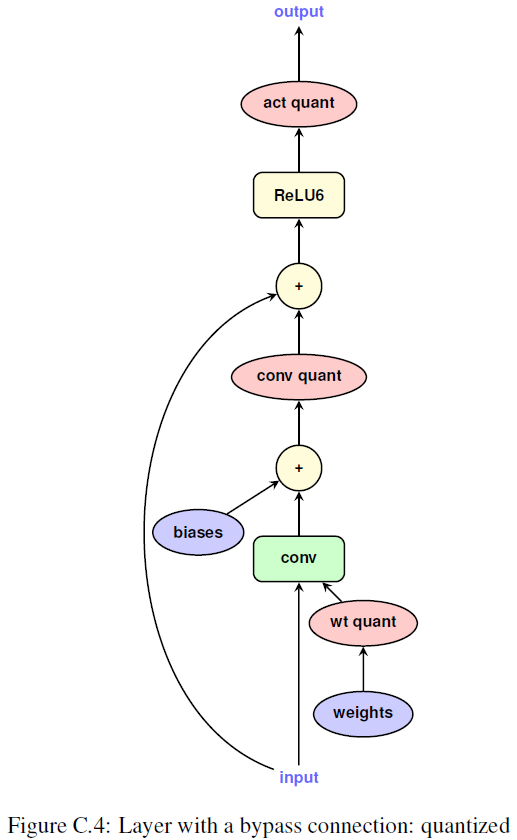
layer with bypass
- origin
- quantized
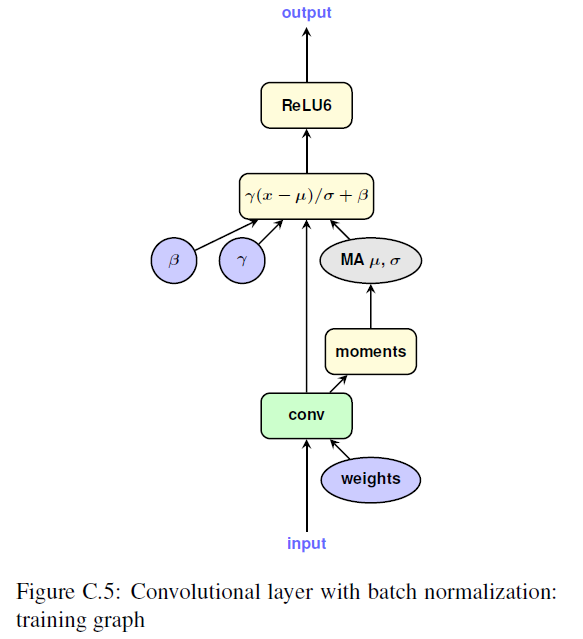
convolutional layer with batch normalization
- training
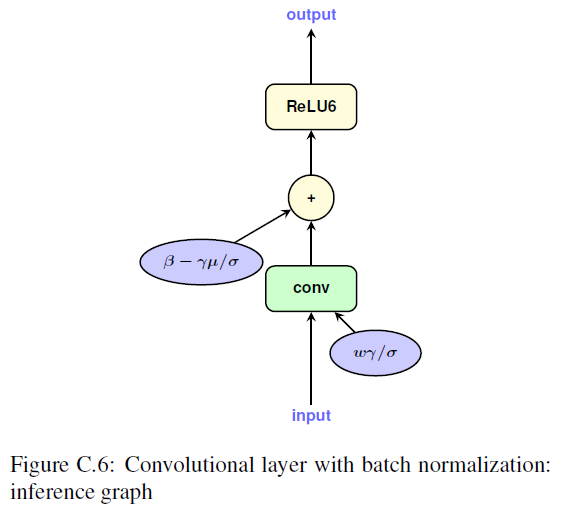
- inference
- training with fold
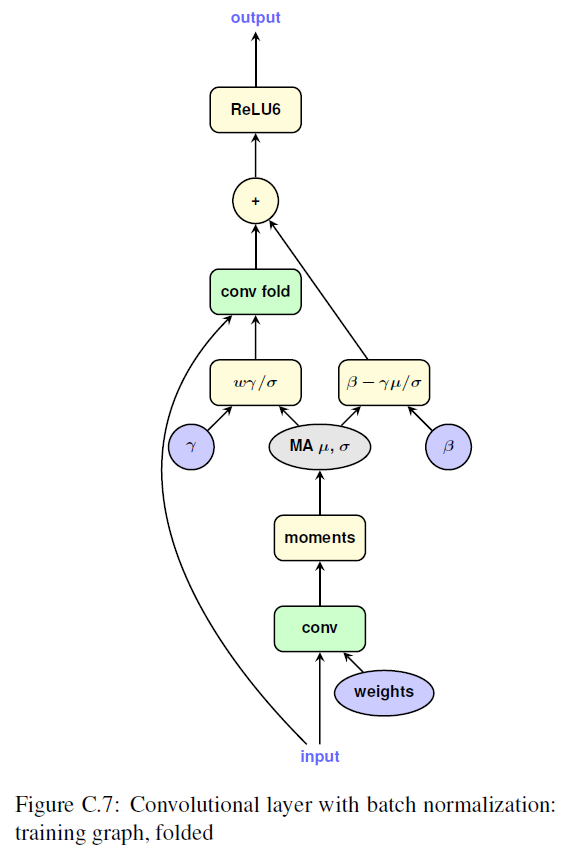
- training with fold quantized