Automatic Differentiation of PyTorch

自动求导概述

参考文献： Automatic Differentiation in Machine Learning: a Survey
目前用于求导的方法大致可以分为四类：

手动解析并代码实现
数值求导 (numerical differentiation), 使用有限的微分近似
符号求导 (symbolic differentiation), 使用代数表达式进行计算
自动求导 (automatic differentiation, also called algorithmic differentiation) 自动求导与数值求导、符号求导两者都不同，如果没有详细的了解的话，容易将自动求导归为数值求导。事实上，自动求导只提供一个数值的结果，并不能像符号求导一样提供一个完整的表达式，但它也确实是根据符号求导的规则进行，通过反向追踪表达式的运算过程实现求导。因此，自动求导兼具了数值求导与符号求导两者的特性。

数值求导的表达式如下：

$$
\frac{\partial f({\mathbf x})}{\partial x_i} \approx \frac{f(x-h {\mathbf e}_i)-f({\mathbf x})}{h},
$$
其中 ${\mathbf e}_i$ 是第 $i$ 单位向量，$h \gt 0$ 是一个小的步长。

符号求导主要根据一系列的求导规则进行变换，例如

$$
\frac{d}{dx}(f(x)+g(x)) \leadsto \frac{d}{dx}f(x) + \frac{d}{dx}g(x)
$$

或

$$
\frac{d}{dx}(f(x)g(x)) \leadsto (\frac{d}{dx}f(x))g(x)+f(x)(\frac{d}{dx}g(x))
$$

从优化的角度，符号求导可以给出问题的内部结构，并用于结果分析。然而，符号求导也容易得到冗长的符号表达式，导致计算困难。

自动求导

自动求导依赖于所有的数值计算都是由有限的元操作构成，并且这些元操作的求导是已知的。依据链式法则，可以将所有组成操作的求导过程联系起来，完成整体的求导。自动求导的模式包括：前向模式以及反向模式。

以 $f(x_1,x_2)={\rm ln}(x_1)+x_1x_2-{\rm sin}(x_2)$ 的求导为例子。其计算过程可以由下图表示。

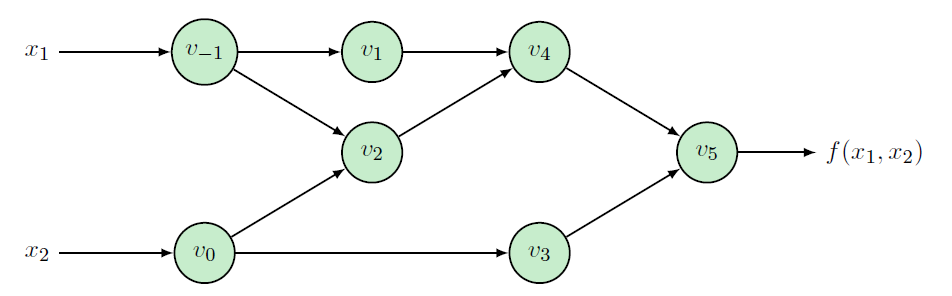
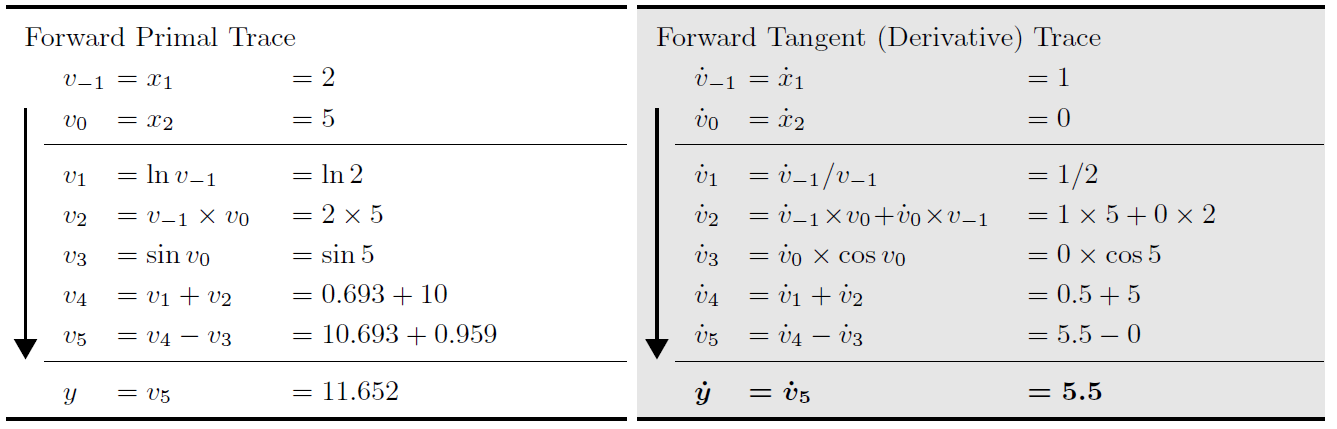
前向模式求解过程：

反向模式求解过程：

PyTorch 自动求导

在PyTorch中的自动求导是tape-based autograd，换句话说是基于类似反向模式的自动求导。通过动态的构建运算图，然后反向传播对各个成分进行求导。在PyTorch中，基本的元操作的求导过程已经写好在程序中，如：

class Sinh(Function):

    @staticmethod
    def forward(ctx, i):
        ctx.save_for_backward(i)
        return i.sinh()

    @staticmethod
    def backward(ctx, grad_output):
        i, = ctx.saved_variables
        return grad_output * i.cosh()